Before we come to the approach lets understand recursion by a small example:
Recursion is like opening a nesting doll. Each time you open one, there's a smaller doll inside. You keep going until you reach the smallest doll, just like solving smaller instances of a problem until you reach the base case in programming.
So basically you apply recursion on those problems where repeated patterns are in the question to reach that one final answer, like wise when searching for an element in a sorted list of 100 integers, using a recursive approach can lead to clear and compact code.
Recursion contains 3 main terminologies
- Function call 2. Base condition 3. Stack
FUNCTION CALL : Recursion has something called as function call. You write your problem logic under a new self created function, and call the same function within itself.
As recursion is breaking down the problem, so you would need to run the logic many times for each part of the problem, right?!! so instead of writing this function each time you just use this function as a call, so that you run this function logic where ever you want in the code.
BASE CONDITION : This data tells at which point recursive loop should end. If base condition is not mentioned then recursion will have an endless loop and will exceed the time limit which can also lead to stack overflow.
STACK: These function calls are stored in stack. The stack starts to get empty when the recursion reaches its base condition.
NOTE: The function call returns to where it was called. (See fig 4.0)
RECURSION requires 5 steps to solve any problem:
Lets understand each steps with an example problem:
- Observe the problem and see if it can be broken down into further sub problems
problem: Count the number of zeros(0's) in a number . Suppose the number is 10203040
The problem of finding the number of zeros in a number can be broken down into subproblems because it naturally lends itself to a digit-by-digit analysis. By examining each digit of the number separately and counting zeros encountered, we can solve the problem recursively. This approach allows us to divide the problem into smaller, more manageable parts, making it easier to understand and implement.
Take pen and paper and draw the recursive tree
Let's see what parameters should be taken for this problem.
Variables that are crucial for the function's operation and need to be accessed outside of it's scope should be included as parameters. This ensures that the function can receive specific values each time it's called.
In this case, it's number & count.
NOTE: The parameters will vary for each problems.
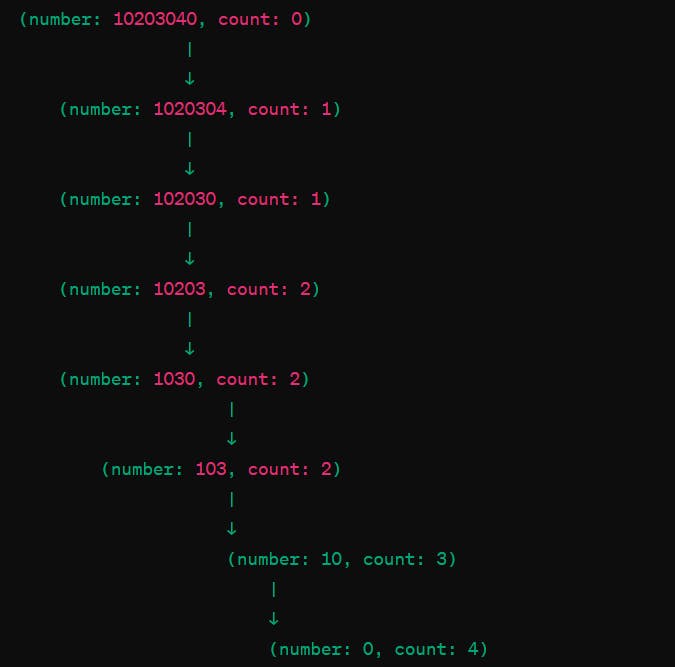
See what the base condition is
In this case, it's when (number == 0) you get your total count. So that's going to be your base condition.
See the flow of the function in the tree and how they will be getting into stack
STACK (FIG 4.0)

Write the recurrence relation (if needed)
The important things to observe :
The Parameter : In this case the number and the count, is the parameter( int n , int c)
Return type : return type is int (as your returning the count in integer data type)
Variable that will come inside the body : when the scope of the variable is only for that particular function, you declare and initialize the variable within that function.
(in this case we require no such variable).
NOTE: These 3 points vary upon different problems.
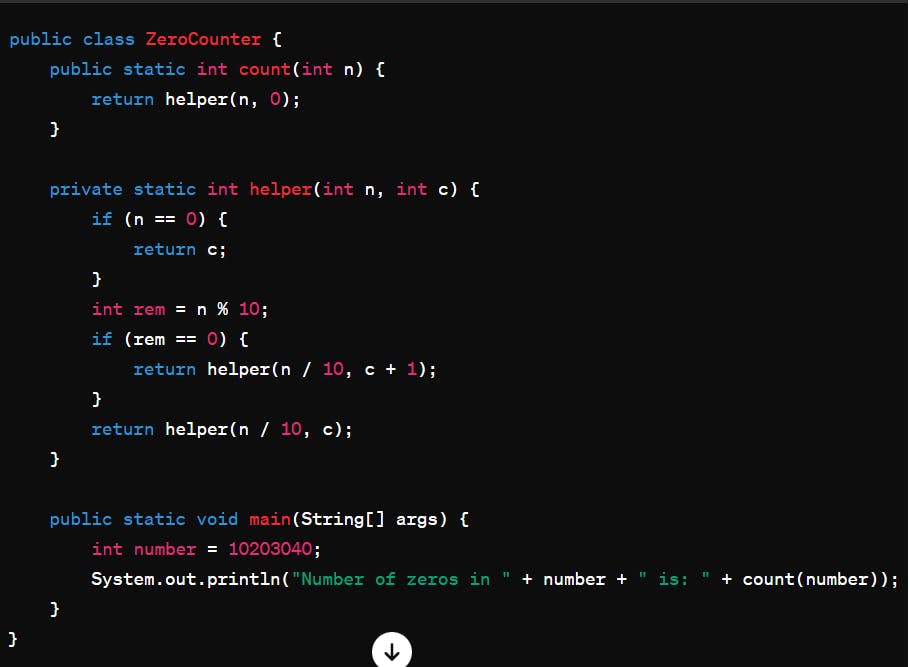
JAVA CODE: Seeing the 5 steps and the 3 observations, now your fine to code!!
END!!
My next blog will be on, the common patterns to use for every subsequence problems using recursion.
Do follow for more such tech contents !!
thank you, happy coding!!
